More Info
Formwork for concrete shells needs to provide a rigid shuttering onto which concrete can be poured and allowed to harden. They are typically complex and unique. Often they cannot be reused, require foundations, and are labour- and material-intensive. Therefore, formworks for concrete shells are expensive and wasteful. Tile vaults are unreinforced masonry structures made of thin bricks (tiles) and fast-setting mortar. They can be constructed without the need for a formwork, except for along their boundaries, making them inherently more economic. The use of tile vaults as permanent formworks for concrete shells would reduce cost and material waste during the construction of shell structures with complex geometry. The combination of masonry and reinforced concrete creates a composite structure with characteristics that require new calculation methods and models to deal with specific features of the system.
This research describes a new method to safely design doubly curved, concrete-reinforced, tile-vaulted structures, and assess their strength and stability against external loading. It is a method based on limit analysis, but taking into account the strength and bonding capacity of the joints and the steel reinforcement by virtually increasing the thickness of the structure accordingly. Therefore, the method provides graphical and intuitive results and offers a viable extension to reinforced masonry structures and fully three-dimensional problems.
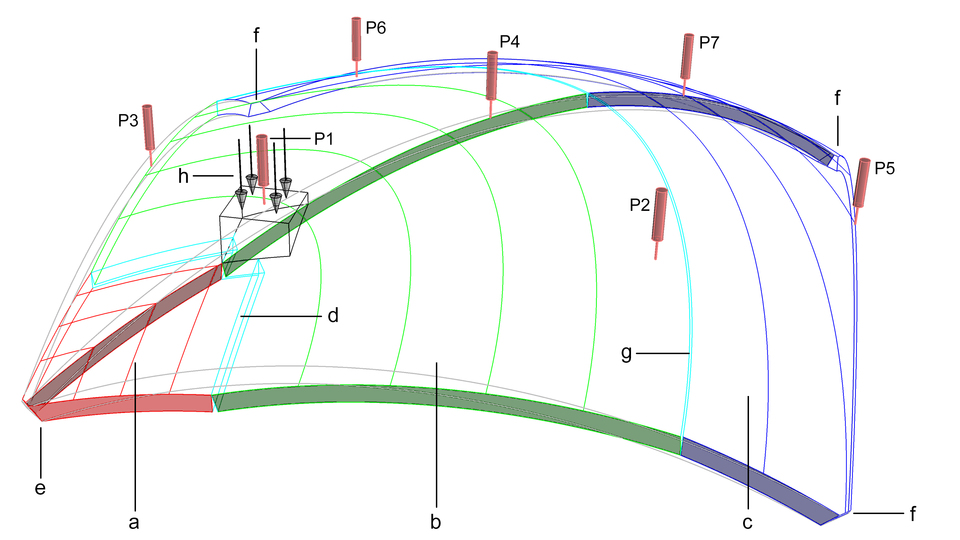
The values of the material properties required to calculate the new virtual thickness are obtained from experimental tests on material samples. Tests on full-scale prototypes are also performed in order to verify the load-bearing capacity predicted with the virtual thickness and thus validate the method. Non-linear Finite Element Analyses of the prototypes are carried out in parallel. The experimental tests on material samples supply the material properties for the numerical models and the load testing of the prototypes allows for their calibration. These FE analyses provide supplementary information about stress distributions, reactions and force flow in the structure, which can be used as a basis for the definition of force patterns for the 3D extension of the method. Moreover, calibrated FE models of additional and more complex geometries allow further validation of the new equilibrium method.