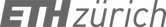Historically, stone cutting of masonry architecture involved expertise in structural and geometric analysis of architectural shapes. Master builders and mathematicians developed intricate design strategies for domes, vaults and bridges such that blocks could be assembled into self-supporting constructions (Figure 1). Contemporary innovations in structural form-finding and fabrication techniques are leading to design of freeform masonry architecture [Block and Ochsendorf 2007; Vouga et al. 2012; Rippmann et al. 2012]. These new forms do not fit to recognisable topologies or primitives, creating new challenges in laying out tessellation patterns. Such patterns must fulfill structural requirements of transferring loads in compression-only equilibrium while addressing certain fabrication constraints. Further, it is desirable from a design perspective to layout elegant patterns with blocks that are uniform, and smooth. Simple sides are furthermore desirable for ease of fabrication and assembly. While new computational tools are becoming available for structurally informed and construction-aware panelisations of architectural surfaces [Schiftner and Balzer 2010; Panozzo et al. 2013; Pietroni et al. 2015], these algorithms aim for automatic generation of a single ‘global optimum’. We argue that for practical application as a design tool, there is a need for ‘controllable’ optimisation: designers must be able to explore variations in block patterns that adhere to design preferences.
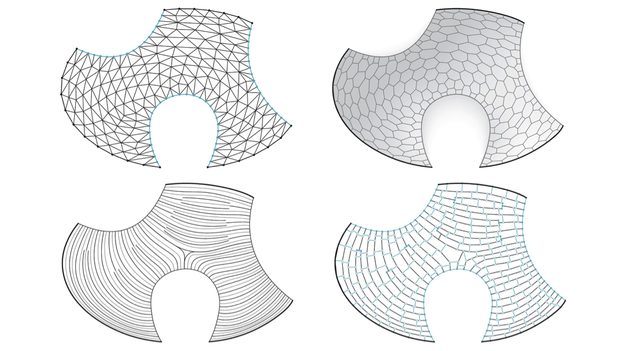
We present two discretisation approaches for given thrust surfaces, allowing for various degrees of user control during the tessellation design process. Both methods are based on a simple set of geometry rules, derived from the analysis of historic techniques, structural requirements and fabrication constraints [Rippmann and Block 2013; Rippmann 2016]. First, we introduce a tessellation approach based on primal, anisotropic triangular meshes and their dual counterparts (Figure 2a). The approach requires little manual modelling due to the increased level of automation, which makes it relatively easy for less experienced designers to generate informed tessellation geometries. Second, an alternative tessellation approach based on transverse cutting curves is presented (Figure 2b). The procedural approach can be controlled carefully through individual, computer-assisted, stepwise optimisation and thus especially suits the tessellation design of intricate vaulted surfaces.
Using these methods, we address the structural stability of the form, by optimising the tessellation based on the “flow of forces”. We interpret internal forces as a vector field and use this as a directional constraint, to ensure a rigid bond and prevent sliding between discrete block geometry. Further, modern stone-cutting technology and material-specific tolerances for registration and fitting accuracy of the blocks are addressed by optimising and controlling the dimension and shape of the tessellation units.
Finally, we compare and discuss the feasibility of both discretisation methods applied on the tessellation design of the “Armadillo Vault” (Figure 3) [Rippmann et al. 2016]. The freeform vault has a span of 16 metres, is comprised of 399 individually cut limestone voussoirs, unreinforced and without mortar, and was exhibited at 15th International Architecture Exhibition - La Biennale di Venezia.